This article was first published in American Rifleman, May 1965.
By Dr. Harold 0. Davidson
Dr. Harold 0. Davidson, a professional engineer with a doctorate in industrial engineering, is President of Davidson, Talbird & McLynn of Bethesda, Md. His personal research into longrange shooting problems is based on shooting experience in the field and on experience in military weapon system effectiveness analysis. He is a member of the Scientific Advisory Group of the Army's Combat Developments Command.
In recent years the magnum rifle has gained considerable popularity for North American hunting. What accounts for the trend? Just what does the magnum offer the hunter?
Claims are made that 500- and 600- yd. kills are pretty common, which implies that they are comparatively easy.
The only data that really demonstrate the capabilities of a weapon are the ballistic data. Makers have not always given velocity, energy, or trajectory data beyond 300 yds. Shooting at ranges up to 500 or 600 yds. is sheer guesswork unless the shooter knows the performance of his weapon and learns how to apply this knowledge to his shooting.
Our purpose here is to examine the capabilities of high-velocity magnums for long-range shooting, and the level of marksmanship and range estimation skills necessary for such shooting.
Two main groups of factors determine the over-all effectiveness of hunting firearms. The more important is a combination of exterior ballistic performance of the weapon and marksmanship skills of the hunter. These together determine his ability to put the impact in a vital area of the target. The second group of factors, including bullet design, weight, and striking energy, determines what happens at the point of impact-the lethal effect of the bullet. Providing the bullet is of the proper design for the particular use so that its energy is delivered within a vital area of the target, the lethal effect of the bullet is closely related to its kinetic energy. The bullet's kinetic energy actually has 2 components-one due to its forward movement, and the other due to its rotation. The equation for calculating total bullet energy is:
E = ½ mv2 + ½ mk2 w2
where 'm' is the bullet mass (weight in grains ÷ 225,000)
'v' is the velocity (feet per second)
'k' is the radius of gyration of the bullet about its longitudinal axis (feet)
'w' is the angular or rotational velocity (radians per second)
When we apply this formula to actual problems, we immediately find that the rotational energy is only a few tenths of 1% of the total and may therefore be neglected. This gives the usual formula for bullet energy, ½ mv2, which for ease of calculation can be written:
bullet weight (grs.) X velocity2 (f.p.s.)
450,000
We can thus dispel one source of confusion that has been advanced in words such as these:
"Rotational speed also plays a big part in destruction of tissue as the jagged ends of the jacket, once they start to expand, act just like a buzz saw and their terrific rotational speed throws pieces of jacket and lead core in all directions." 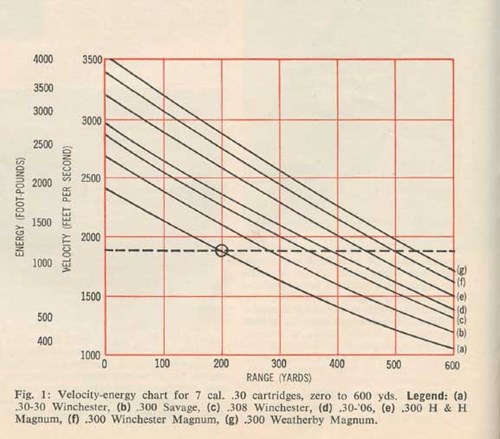
This idea seems plausible if we look only at rotational speed, which may be on the order of 200,000 r.p.m. at the muzzle of a high-velocity rifle. But the surface velocity in the direction of rotation for a cal. .30 bullet at this speed is actually less than 300 f.p.s., and the rotational energy is barely 10 ft.-lbs. For further appreciation we might give a moment's consideration to high-speed turbine-driven dental drills. Despite very high rotational speeds, comparable with the above, these drills have extremely low angular momentum and are easily stalled. The plain fact is that rotation of the bullet has almost nothing to do with tissue destruction because there is no significant amount of energy involved in the rotation.
As an initial step toward the second objective, remember that the 'super knockdown' or 'explosive killing power' that a high-velocity magnum may deliver at short to moderate ranges does not exist at long range. The moment the bullet comes out of the muzzle, aerodynamic drag begins to take its inexorable toll, which for a 150-gr. cal. .30 bullet is roughly a 12½ % loss in velocity for every 100 yds. of travel. These laws of aerodynamics affect all bullets, so that at 400 yds. some 34% to 40% of the original velocity and 55% to 60% of the muzzle energy have been lost in the air. In short, there is no long-range super knockdown because there are no high-energy bullets remaining after 400 yds.
Velocity and energy losses
An over-all picture of velocity and energy losses from zero to 600 yds. for 7 cal. .30 cartridges is given in Fig. 1. The curves charted are based on the standard factory 150-gr. bullet loads, but they are calculated for comparative purposes on the assumption that all cartridges are loaded with the same type of bullet (which is not actually the case).
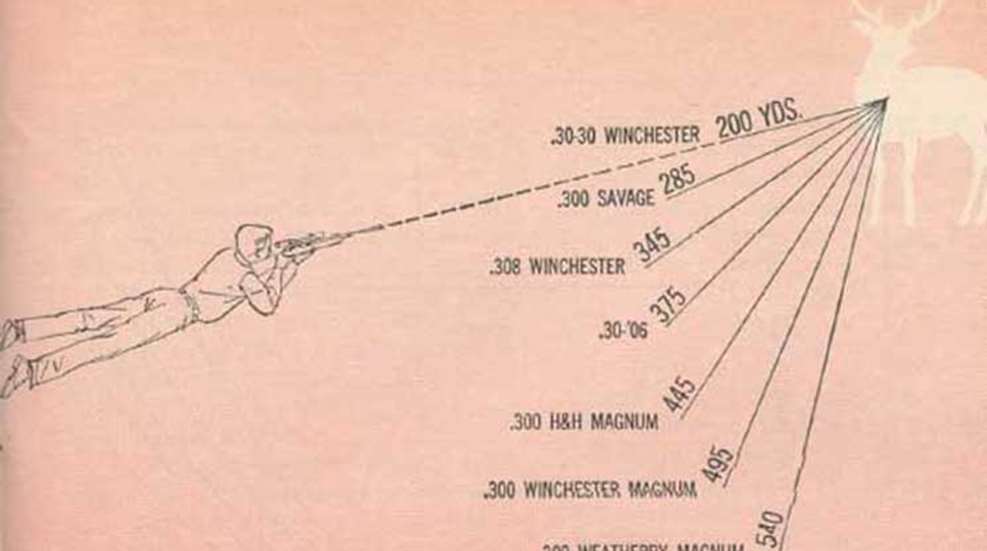
The circled point on the .30-30 curve indicates the velocity at 200 yds. as about 1900 f.p.s. At just under 1200 ft.-lbs. energy, the .30-30 at 200 yds. is scarcely a block-buster. To be sure, well-directed .30-30 bullets have killed every species of North American game at ranges up to 200 yds. and more. However, most experienced sportsmen favor weapons of considerably more power than the .30-30 for hunting elk, moose, and large bear—no matter at what range the shot is taken.
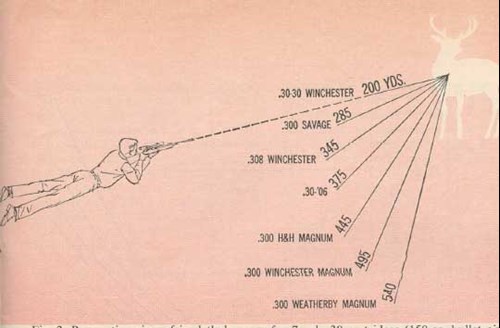
Each of the other 6 cartridges loaded with the same 150-gr. bullet will at some particular range become equivalent to the .30-30 in lethality. In Fig. 1, this iso-lethal range for each cartridge is indicated by the dotted line.
Fig. 2 illustrates how increased muzzle velocity extends the range from which a given lethal effect can be delivered. It is clear that the hunter with a magnum at around 500 yds. is using a rifle of no greater lethality than a .30-30 at 200 yds. The requirements for placement of shots with a magnum at 500 yds. are then no less severe than those with a .30-30 at 200 yds.
To determine the ease or difficulty in meeting these requirements, we must analyze our first and more important group of factors-exterior ballistic performance of the weapon and marksmanship skills of the hunter.
In making this analysis, it is necessary to identify the factors that influence placement of the bullet, and calculate their effects on accuracy.
Assume the rifle is precisely zeroed to a known range, in this case the iso-lethal range. The assumption is justified because we can in fact make the zeroing error negligibly small (whether or not all hunters actually do so), whereas we cannot be sure of eliminating the other 3 sources of error-deflection error, range error, and dispersion.
Deflection errors are caused by incorrect allowances for the effect of wind or incorrect estimates of the lead on running game. We will pass by the problem of lead errors since it will soon be clear that long-range shooting at running game is a sport for only the most skillful marksmen. A substantial proportion of long-range opportunities are stationary targets which present no deflection problem except wind.
To get a feel for the problem, consider a moderate crosswind of 10 miles per hour ( 14.7 f.p.s.). This wind will deflect the magnum bullet about 2 ft. at 500 yds. By comparison the .30-30 bullet will deflect less than one ft. at 200 yds. It appears that despite the magnum's initial high velocity there is considerable guesswork left in the matter of wind corrections under certain conditions. Of course the wind conditions will frequently be better than assumed in this example, but at times they may also be worse.
It is true that at equal ranges the .300 Magnum is somewhat less sensitive to wind deflection than the .30-30, but our purpose is to find what the magnum capabilities are for accurate shooting up to 500 and 600 yds. Evidently, wind errors at these ranges may well become large enough to be troublesome.
Range errors arise because allowance must be made for drop. Despite the flat-shooting qualities of magnums, the sad fact is that the law of gravity is no kinder to magnum bullets than it is to any other kind. Every bullet falls the same amount per second of flight. Over equal ranges, the fastest bullet will, of course, fall the least and therefore have the flattest trajectory. The situation is quite different, however, when we compare weapons at their iso-lethal ranges as shown in Fig. 3, and assess the effect of errors committed in estimating these ranges correctly.
Errors in range estimation
In Fig. 3 we have segments of the trajectories from -20% to +20% of the iso-lethal ranges for the 7 cal. .30 cartridges indicated previously. It is readily apparent that the shooter with a .30-30 at 200 yds. who can hold his range estimation errors within plus or minus 20% is in pretty good shape. When he lines up on a target, he can expect that his impact point will not be more than about 3" or 4" off due to range error. But give the same man a magnum at 500 yds. or so, and he has a real problem. A 20% overestimate or underestimate of range will just about guarantee a miss. If he cuts his error to 10%, he can still be off by some 11". 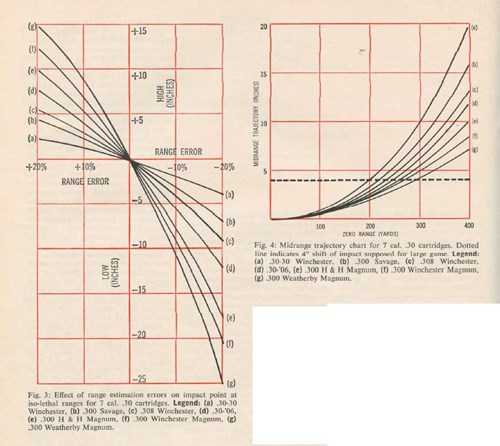
To put the shot within 4" of his intended impact point he has to reckon the range to about 4%. Therefore, shooting magnum rifles at long ranges requires considerably greater relative accuracy in the estimation of range than does shooting low-power rifles at moderate ranges.
With this fact in mind, consider the viewpoint of the shooter who is not particularly keen on range estimating and takes them as they come. First we must decide how much shift in the impact point above or below point of aim can be tolerated without serious risk of missing the vital area. This, of course, depends on the target—it is not the same for deer as it is for varmints.
Suppose, for example, that with large game a 4" shift of impact point can be accepted. With a chart as shown in Fig. 4, it is an easy matter to determine the range at which we should sight-in the rifle. On the vertical scale at the left of the chart, first locate the line corresponding to the 4" shift (or whatever other maximum deviation is acceptable). Follow this line horizontally to the right until it intersects the curved line for the cartridge used. From the point of intersection, drop down to the range scale and read off the range.
In this example we find that the .30- 30 should be zeroed at 200 yds., whereas the .300 Weatherby can be zeroed at 290 yds. under the same restriction. Now, if we accept the same 4" displacement of the impact below the line of sight, the pointblank range will be about 20% greater than the zero range—which is to say, about 240 yds. for the .30-30 and 350 yds. for the .300 Weatherby. In this example the magnum provides a good 100 yds. over the pointblank range of the .30-30, but only about 50 yds. over the .30-'06. We say 'only' 50 yds. because all the excitement over flat-shooting magnums might have led some of us to expect a much bigger difference. At the same time it should be noted that in western shooting a good bit of game can be located in that 50 yds. just beyond 300 yds. The magnum gets to 350 yds. with almost 30% more remaining energy than the .30-'06 has at 300 yds.
It seems, then, that the high-velocity magnum does extend point-and-shoot ranges by a useful amount-but not to anything like 500 or 600 yds., and not without penalty as a consequence of dispersion which increases with range.
Dispersion ultimately sets a practical limit to long-range shooting no matter what the muzzle velocity might be. It is the consequence of our inability to produce and use rifles and ammunition with absolute precision, so that bullets impact on exactly the same point.
Minutes of angle is a usual way of describing dispersion. A rifle that will consistently deliver 1" groups at 100 yds. is said to have one-minute accuracy. Actually, one is fortunate to find a hunting rifle that will give a one minute bench-rest grouping with no tune-up. Under field shooting conditions many 5-shot groups run over 3 minutes. The shooter who can stay consistently around 2 minutes is a fairly accomplished rifleman who usually hangs his tag on anything that gets in his scope at normal shooting ranges.
In considering the effects of dispersion, we should take particular note that it increases practically in direct proportion to range. Hence, a 2-minute group that corresponds to 2" at 100 yds. expands to 6" at 300 yds., and to slightly more than a foot at 600 yds. Similarly, a 3-minute group spans a bit over a foot and a half at 600 yds.
The basic philosophy in field shooting ought to be that the first shot is by far the most important one. It would be advantageous then if we could determine the likelihood of putting this first shot within a target of some given size at various ranges.
Data on first-round hits
This problem of first-round hits has in recent years received serious attention with respect to military targets, and the necessary experimental and analytical means have been applied to it. Some of the information obtained is here boiled down to a do-it-yourself recipe for the rifle shooter.
The first step, a simple thing the shooter can do for himself, is to determine his reference group. The recipe is extremely simple-just assemble a collection of 5-shot groups and arrange them in order of size. The middle group is the reference group.
There is no point in putting any bench-rest groups in this collection if a bench rest is not used in game shooting. To get a good estimate of dispersion under field conditions the 5-shot groups should be collected under field conditions. Do not use a sand bag. Get out of shooting position after each shot and then back into it for the next. Make separate collections for prone, sitting, kneeling, and offhand positions, and select a reference group for each because the dispersions probably will be different. Finally, it is not necessary that all groups be shot at the same range provided they are all converted to equivalent group size at some selected range—say 100 yds. (In this case the size of each 200-yd. group would be divided by 2, a 300-yd. group by 3, and so on.)
Now we have the basic information, which is the size of the reference groups for each position at some given range. This size is identified by the symbol gr.
The next step is to determine the size of the target area. While there are methods for solving the problem for targets of any shape, the calculations become quite tedious. It is simplest, and in many instances sufficient, to assume a circular target and designate its size by the diameter D.
Then D should be divided by g, which is the dispersion factor for the range of interest. If the range happens to be the same range for which we have determined the reference group, then g = gr. If it is some other range, X, and the reference group range is R, then
This text will need to be fixed as an equation:
g = gr
X/R
After finding the ratio D/g we can look to Table 1 for the first-round hit probability, which is designated by the symbol P. The figure 2/ 100 means that because of dispersion errors the odds are about 2 in 100 of hitting the specified target at the selected range. Many textbooks use the term probability measured in decimals, instead of odds. Thus, a probability of .02 is the same thing as 2/100 odds.
Now that we have a method for figuring dispersion errors, let us see how much they affect the rifleman's ability to place his shots as the range increases. For this purpose let us take an 8" circle as the vital target area for game such as antelope or small deer, and 12" for larger game; then consider different degrees of dispersion as represented by 2", 4", and 6" reference groups at 100 yds. By applying the method just described we obtain the accompanying Table 2 of odds for a first-round hit in the target area at ranges from 100 to 600 yds.
No substitute for skill
These results reveal that we do not have a rifle that will turn the casual sportsman into an expert marksman at ranges up to 500 or 600 yds.
At ranges of 100 yds. or so it is a different story. Provided he does not get rattled, a shooter with moderate skill has about as good a chance of putting his shot in a 12" stationary target as the expert. But the payoff on skill increases with range, so that at long ranges skill counts for a good deal more than a few hundred feet extra muzzle velocity.
Now that we have seen how dispersion becomes a limiting factor on ability to place the bullet even if range estimation errors were eliminated, we can turn back to the realistic situation-the combined effect of dispersion with range estimation and deflection errors.
As indicated previously, both range and deflection errors have the same kind of effect-namely, a displacement of effective aiming point. This means that whatever method we can find for combining range errors with dispersion effects will also work on deflection errors. Hence, we can simplify matters by concentrating for the moment on range errors and dispersion. If we start out by considering a simple dispersion effect as pictured in Fig. 5(a), the addition of a range error alters the situation as shown in Fig. 5 (b). This will give a lower first• round hit probability, which we can calculate for any given displacement.
Let us take a specific case from Table 2 and see how the combined effect compares with the dispersion effect alone. Using, for example, a 12" target area at 500 yds., and gr = 4" (100 yds.) we have a .52 first-round hit probability; which is to say 52 in 100 odds. Now assume that we have underestimated the range by about 5%, which means ' that the actual range is around 520 yds. instead of 500. The trajectory chart for the particular .300 Magnum load being used indicates 6" of drop between 500 and 520 yds., so the effective aiming point is 6" below the center of the target. This displaces the reference group circle in the manner shown in Fig. 5(b), and reduces the hit probability from .52 to .36. In other words, it cuts the chances to about two-thirds what they were without this range error.
The consideration thus far has been only the effect of one particular range error of a specified amount. In reality the range error varies from one situation to another and cannot be predicted for any specific case. As shown in Fig. 5 (c), we sometimes overestimate, at other times underestimate, and occasionally estimate correctly. If we knew the odds of each particular range error, we could multiply the odds of this error occurring by the odds of hitting the target if that error occurred, repeat this process for every possible error, and finally add all the results together to get an over-all first-round hit probability for the combined dispersion and range error effects. But since we have no good data on range errors in hunting we will have to assume several hypothetical cases and hope they are fairly representative of degrees of skill in range estimation. Anyone who has accurately determined his own skill in range estimation can then select the hypothetical case which approximates his own abilities. 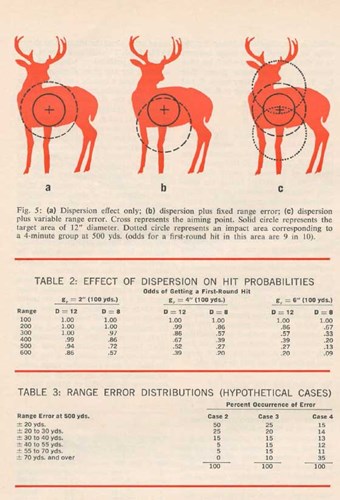
For this purpose assume 3 simple cases in addition to the No Error or dispersion-only case which has already been considered. We will define each case in terms of the odds or relative frequency of occurrence of errors of a given amount, as shown in Table 3.
HypotheticaI cases defined
We are hesitant to suggest how these sample cases might correspond to actual range estimation abilities. Case 2 was selected to represent an exceptionally high degree of skill, which may in fact be virtually unattainable. We think Case 3 represents well above average skill. Case 4 was selected with the idea that it might correspond fairly closely to an average level of skill, but this supposition may not be correct. Actually it would not be a particularly large or difficult research job to determine range estimation abilities in a representative sample of hunters, and the results would be of considerable interest. If such a project is ever carried out, the actual results can be substituted for the hypothetical cases. In the meantime, these estimates must suffice.
The next step, then, is to multiply the relative frequency of occurrence of each category of range error times the hit probability associated with it; and add these figures together for each hypothetical case, at each range, for each level of dispersion, and for each target size of interest. The result of doing all this is shown in Table 4 for a 12" target area, based on the trajectory of the 150-gr. bullet in the .300 Weatherby Magnum. Results from similar calculations for .30-30 and .30-'06 trajectories are shown in Table 5, for 500-yd. range, along with the .300 Weatherby Magnum data for comparison.
At this point we have enough information to evaluate the comparative influence of marksmanship, range estimation skills, and flatness of trajectory in long-range shooting.
Evaluating combined errors
From the information in Table 4 we see that the formula for an expert longrange rifleman calls for nearly equal proportions of marksmanship and range estimation skills, if our assumptions regarding skill in these calculations are anywhere near the facts. To reach this conclusion it can be noted that for any given combination of ranges and range error, the odds for a hit increase about 2Yz times for a reduction in dispersion from gr = 6 to gr = 2; while for any given combination of range and dispersion the odds for a hit increase by almost the same amount for a change in range errors from Case 4 to Case 2. On an over-all basis, the ratios of odds for an expert rifleman (gr = 2, Case 2 range error) to those for an average rifleman (g, =6, Case 4 range error) are about 4 times better at 400 yds., 5 times better at 500 yds., and 6 times better at 600 yds. There is therefore a large payoff on both marksmanship and range estimation abilities, even with the benefits of a high-velocity magnum taken into account. That these benefits are in fact substantial is shown by Table 5, which is about as clear a recommendation as we could want in favor of the high-velocity magnum for longrange shooting.
One additional point of interest comes to light in these results. If an expert rifleman (gr = 2 and Case 2 range error) changes from a .30-30 to a magnum he gains 27 additional chances in 100 of getting a first-round hit (since .62 - .35 = .27). By comparison, an average rifleman (gr = 6 and Case 4 range error) gains only 6 chances in 100 (.12 - .06 = .06). This illustrates the fallacy in the idea that high velocity is a satisfactory substitute for range estimation skills.
We have now seen the kind of effect we get from the combination of dispersion and range errors, and have noted also that the method used for combining these factors will also work for wind deflection errors. What is not yet clear is how to make some reasonable guesses as to the actual wind deflection errors in field shooting. Deflection errors can be assumed negligible in still air to gentle breezes, so that the results already calculated are applicable. They should also be negligible in the case of a rather strong wind that is blowing from dead ahead or from behind the shooter. In other circumstances, deflection errors have some effects—the greater the wind force, the greater the errors will be.
As noted previously, the 150-gr. bullet from a .30 magnum will be deflected on the order of 2 ft. at 500 yds. in a moderate crosswind of 10 m.p.h. Now suppose that small errors are more frequent than large ones, and that the maximum possible error is half the actual deflection. Under these assumptions the separate effect of deflection errors will be similar to those of Case 3 range error, and the combined effect will be shown in Table 6. The first column in this table is taken from Table 4, to provide a comparison. The results indicate that deflection errors caused by a moderate crosswind may reduce the odds of a first-round hit by something like 20% to 30%.
Obviously, results based on the kind of educated guesses we have had to make cannot be exact. The methods for calculating these results can, however, be refined to any desired level of precision so that more accurate results can be calculated whenever there is better basic data available. Even so, the results given here do justify some valid general conclusions.
First, let us re-emphasize the basic fact that a high-velocity magnum at 500 to 600 yds. is comparable in lethality to a .30-30 at some 200 yds. It therefore cannot be considered adequate for long-range shooting of any game for which the .30-30 at 200 yds. would be judged inadequate.
The second major conclusion concerns bullet placement. We have seen that there exists no super killing power to compensate for poor placement at long ranges. It is also clear, from the results obtained, that the chances are relatively poor for effectively placing a second shot in a running wounded animal at long ranges. For these reasons, placement of the first shot in a vital area is especially important. Marksmanship and range estimation skill are prerequisite to high probabilities for a successful placement, no matter what type cartridge is employed.
To amplify this final point, consider the hunter of modest skills who has about one chance in 10 (.10 odds) of placing the first shot in a vital area at a 500- to 600-yd. range. Since the nonvital areas of the target are larger than the vital areas, he and his brethren will wound more game than they kill with the first shot. Even with the unlikely assumption that opportunities for second and third standing target shots will be available in these cases, there will still be only one chance in 5 that the second or third shot will hit a vital area. 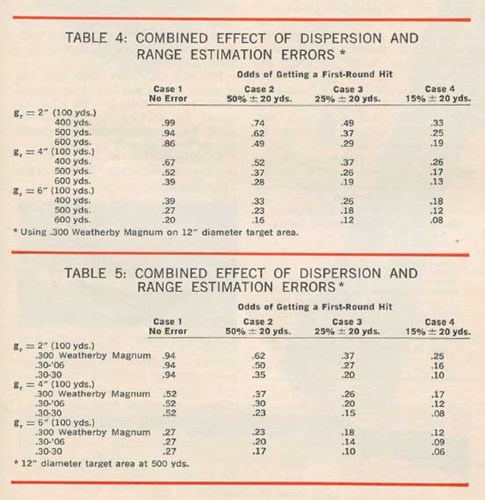
 Success often misleading
Success often misleading
It is clear that if enough hunters with this level of skill are encouraged to blaze away at these 500- and 600-yd. ranges, around one out of 10 will by chance connect with the vital target area. The hunter enjoying this fortuitous experience may well be convinced that he has indeed found some kind of super weapon. In the greater number of cases in which the long shot is missed or messed up, the shooter accepts the result as normal and sees no reason to make it a matter of record. Because of this bias, it is entirely possible to accumulate a collection of sincere testimonials which nevertheless are a gross misrepresentation of the facts as determined by objective analysis. The effect, unfortunately, is to encourage more long-range shooting by hunters who in most instances would be better advised (in the interest of their own success as well as good sportsmanship) to spend a little more time working up on the game before shooting.
The results of our analyses indicate that if a reasonably good marksman with a high-velocity magnum will close the range to about 350 yds. or less he has an excellent chance of putting his first shot in a vital area. The reasonable maximum limit of high-velocity magnums extends beyond this to some 500 or 600 yds. for deer, antelope, and comparable animals. However, a high degree of skill in marksmanship and in range and wind deflection estimation is essential to exploit this capability.





































